In the conic projection the graticule is projected onto a cone tangent, or secant, to the globe along any small circle (usually a mid-latitude parallel). In the normal aspect (which is oblique for conic projections), parallels are projected as concentric arcs of circles, and meridians are projected as straight lines radiating at uniform angular intervals from the apex of the flattened cone. Conic projections are not widely used in small scale mapping because of their relatively small zone of reasonable accuracy. The secant case, which produces two standard parallels, is more frequently used with conics. Even then, the scale of the map rapidly becomes distorted as distance from the correctly represented standard parallel increases. Because of this problem, conic projections are best suited for maps of mid-latitude regions, especially those elongated in an east- west direction.

If you have a VRML-compatible browser installed on your computer, you may want to look at the following 3D virtual model of a cone, halfway between a globe and a conic projection. If you do not have a plugin capable of rendering Virtual Reality Models, you can download e.g. the Cosmo player or the Viscape player.

General characteristics

• Lines of latitude and longitude are intersecting at 90 degrees
• Meridians are straight lines
• Parallels are concentric circular arcs
• Scale along the standard parallel(s) is true
• Can have the properites of equidistance, conformality or equal area
• The pole is represented as an arc or a point

Ptolemy (in A.D.150) made no reference to a cone, but introduced two projections with concentric, circular arcs for parallels of latitude (like conics) but with meridians that are broken straight lines or circular arcs. These projections although conic-like, were not conic.

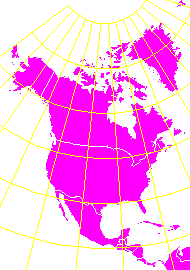	Equidistant or simple conic projection Equally spaced parallels Compromise. Direction, area, and shape are distorted away from standard parallels Equidistant meridians converging at a common point This projection was developed by De l'Isle. It was used for field sheets and some charts of small areas in th 19th century. [Equations]
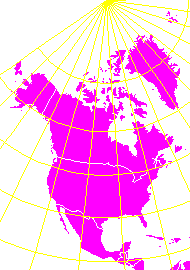	Lambert-Gauss conformal conic projection Conformal. Area, and shape are distorted away from standard parallels. Directions are true in limited areas Developed by J.H. Lambert in 1772. Harding, Herschel and Boole had developed it independently in both spherical and ellipsoidal forms during the 19th century. World War I gave this projection new life, making it the standard projection for intermediate - and large-scale maps of regions in midlatitudes (for which the transverse Mercator is not used). Today it is often used for air navigation maps [Equations]
	Albers equal-area conic projection Distorts scale and distance except along standard parallels. Areas are proportional and directions are true in limited areas [Equations]